Chapter 6 Risk Prediction and Validation (Part II)

6.1 The Brier Score

  • Binary outcomes - \(Y_{i}\) for individual \(i\).

  • Let \(g(\mathbf{x}_{i})\) be a risk score for an individual with covariate vector \(\mathbf{x}_{i}\).

  • If \(g(\mathbf{x}_{i})\) is interpreted as an estimate of the probability that \(Y_{i} = 1\), the Brier score is a measure of the predictive accuracy of \(g(\mathbf{x}_{i})\).

  • For binary outcomes \(Y_{i}\) and risk scores \(g(\mathbf{x}_{i})\), the Brier score is defined as \[\begin{equation} BS(Y, g) = \frac{1}{n}\sum_{i=1}^{n} \{ Y_{i} - g(\mathbf{x}_{i}) \}^{2} \end{equation}\]

  • The Brier score is typically used to compare the accuracy of risk scores.

    • It is hard to tell if a risk score is good just by looking at the Brier score itself without comparing it with other methods.
  • Even if \(g(\mathbf{x}_{i})\) is a class prediction rather than a probability (i.e., \(g(\mathbf{x}_{i}) = 0\) or \(g(\mathbf{x}_{i}) = 1\)), the Brier score can be interpreted as the proportion of “misclassified” outcomes \[\begin{equation} BS(Y, g) = \frac{1}{n}\sum_{i=1}^{n} \{ Y_{i} - g(\mathbf{x}_{i}) \}^{2} = \frac{1}{n} \sum_{i=1}^{n} I\{Y_{i} \neq g(\mathbf{x}_{i}) \} \end{equation}\]

  • The Brier score is a single measure that is affected by both the discrimination and calibration of the risk score.

  • The usual justification for this is to look at the following approximation of the Brier score \[\begin{equation} BS(Y, g) \approx \tilde{BS}(Y,g) = \frac{1}{n}\sum_{s=1}^{S} \sum_{i=1}^{n} a_{is}\{Y_{i} - \bar{g}_{s} \}^{2} \end{equation}\]

  • This approximation assumes \(S\) strata: \([s_{0}, s_{1}), [s_{1}, s_{2}), \ldots, [s_{S-1}, s_{S})\).

  • \(a_{is}\) is an indicator of whether or not the \(i^{th}\) observation falls into the \(s^{th}\) stratum:

    • That is, \(a_{is} = 1\) if \(s_{s-1} \leq g(\mathbf{x}_{i}) < s_{s}\)

  • \(\bar{g}_{s}\) is the average value of the risk score within stratum \(s\) \[\begin{equation} \bar{g}_{s} = \frac{1}{n_{s}} \sum_{i=1}^{n} a_{is} g(\mathbf{x}_{i}) \end{equation}\] and \(n_{s}\) is the number of observation where the risk score is in stratum \(s\).

  • If we let \(\bar{Y}_{s} = \frac{1}{n_{s}}\sum_{i=1}^{n} a_{is}Y_{i}\) be the proportion of 1’s in stratum \(s\), we can simplify the expression for the approximate Brier score as follows: \[\begin{eqnarray} \tilde{BS}(Y,g) &=& \frac{1}{n}\sum_{s=1}^{S} \sum_{i=1}^{n} a_{is}\{Y_{i} - \bar{Y}_{s} + \bar{Y}_{s} - \bar{g}_{s} \}^{2} \nonumber \\ &=& \frac{1}{n}\sum_{s=1}^{S} \sum_{i=1}^{n} a_{is}\{Y_{i} - \bar{Y}_{s} \}^{2} + \frac{1}{n}\sum_{s=1}^{S} n_{s}\{\bar{Y}_{s} - \bar{g}_{s} \}^{2} \nonumber \\ &=& \frac{1}{n}\sum_{s=1}^{S} n_{s}\bar{Y}_{s}(1 - \bar{Y}_{s}) + \frac{1}{n}\sum_{s=1}^{S} n_{s}\{\bar{Y}_{s} - \bar{g}_{s} \}^{2} \nonumber \\ &=& B_{D} + B_{C} \end{eqnarray}\]

  • The quantity \(B_{D} = \frac{1}{n}\sum_{s=1}^{S} n_{s}\bar{Y}_{s}(1 - \bar{Y}_{s})\) is related to the discrimination of the risk score \(g\).

  • To get a sense of why \(B_{D}\) measures discrimination, suppose \(s\) is a stratum where \(s_{s} \leq t\).

  • If the risk score has good discrimination, this threshold should separate most of the “successes” from the “failures”.

    • That is most with \(g(\mathbf{x}_{i}) \leq t\) has \(Y_{i} = 0\) and most with \(g(\mathbf{x}_{i}) > t\) has \(Y_{i}=1\).
    • This \(\bar{Y}_{s}(1 - \bar{Y}_{s})\) is close to \(0\).
    • If this is close to \(0\) for most threholds, \(B_{D}\) will be small.

  • The quantity \(B_{C} = \frac{1}{n}\sum_{s=1}^{S} n_{s}\{\bar{Y}_{s} - \bar{g}_{s} \}^{2}\) is a measure of calibration.

  • For a well-calibrated risk score, the proportion of successes \(\bar{Y}_{s}\) in stratum \(s\) should be close to the average value of the risk score \(g_{s}\) in stratum \(s\).

6.1.1 Brier scores for biopsy data

  • Let’s compute the Brier score using the biopsy data again from the MASS package.
library(rpart)
library(MASS)

data(biopsy)
# Create binary outcome for tumor class
biopsy$tumor.type <- ifelse(biopsy$class=="malignant", 1, 0)
head(biopsy)
##        ID V1 V2 V3 V4 V5 V6 V7 V8 V9     class tumor.type
## 1 1000025  5  1  1  1  2  1  3  1  1    benign          0
## 2 1002945  5  4  4  5  7 10  3  2  1    benign          0
## 3 1015425  3  1  1  1  2  2  3  1  1    benign          0
## 4 1016277  6  8  8  1  3  4  3  7  1    benign          0
## 5 1017023  4  1  1  3  2  1  3  1  1    benign          0
## 6 1017122  8 10 10  8  7 10  9  7  1 malignant          1
  • Let’s try constructing fitted probabilities using three approaches:
    • logistic regression
    • CART
    • random forest
library(rpart)
library(randomForest)

# Fit CART, logistic regression, and random forest
cart.model <- rpart(class ~ V1 + V3 + V4 + V7 + V8, data=biopsy)
logreg.model <- glm(tumor.type ~ V1 + V3 + V4 + V7 + V8, family="binomial", data=biopsy)
RF.model <- randomForest(class ~ V1 + V3 + V4 + V7 + V8, data=biopsy, ntree = 500)
  • Let’s then compute “risk scores” from each method.
probs.cart <- predict(cart.model)
head(probs.cart)
##      benign malignant
## 1 0.9837587 0.0162413
## 2 0.0952381 0.9047619
## 3 0.9837587 0.0162413
## 4 0.0952381 0.9047619
## 5 0.9837587 0.0162413
## 6 0.0952381 0.9047619
# We want the second column of this matrix for the CART fitted probabilities
risk.cart <- probs.cart[,2]

# logistic regression 
risk.logreg <- predict(logreg.model, newdata=biopsy, type="response")

# random forest risk scores
risk.RF <- predict(RF.model, newdata=biopsy, type = "prob")[,2]
  • The in-sample Brier scores for each method are:
    • “In-sample” here meaning we are computing the Brier score using the same outcomes we used to construct the risk scores.
brier.cart <- mean((risk.cart - biopsy$tumor.type)^2)
brier.logreg <- mean((risk.logreg - biopsy$tumor.type)^2)
brier.RF <- mean((risk.RF - biopsy$tumor.type)^2)

round(c(brier.cart, brier.logreg, brier.RF), 4)
## [1] 0.0450 0.0280 0.0056
  • When comparing in-sample Brier scores, CART is the worst, logistic regression is in the middle, and random forest is the best.
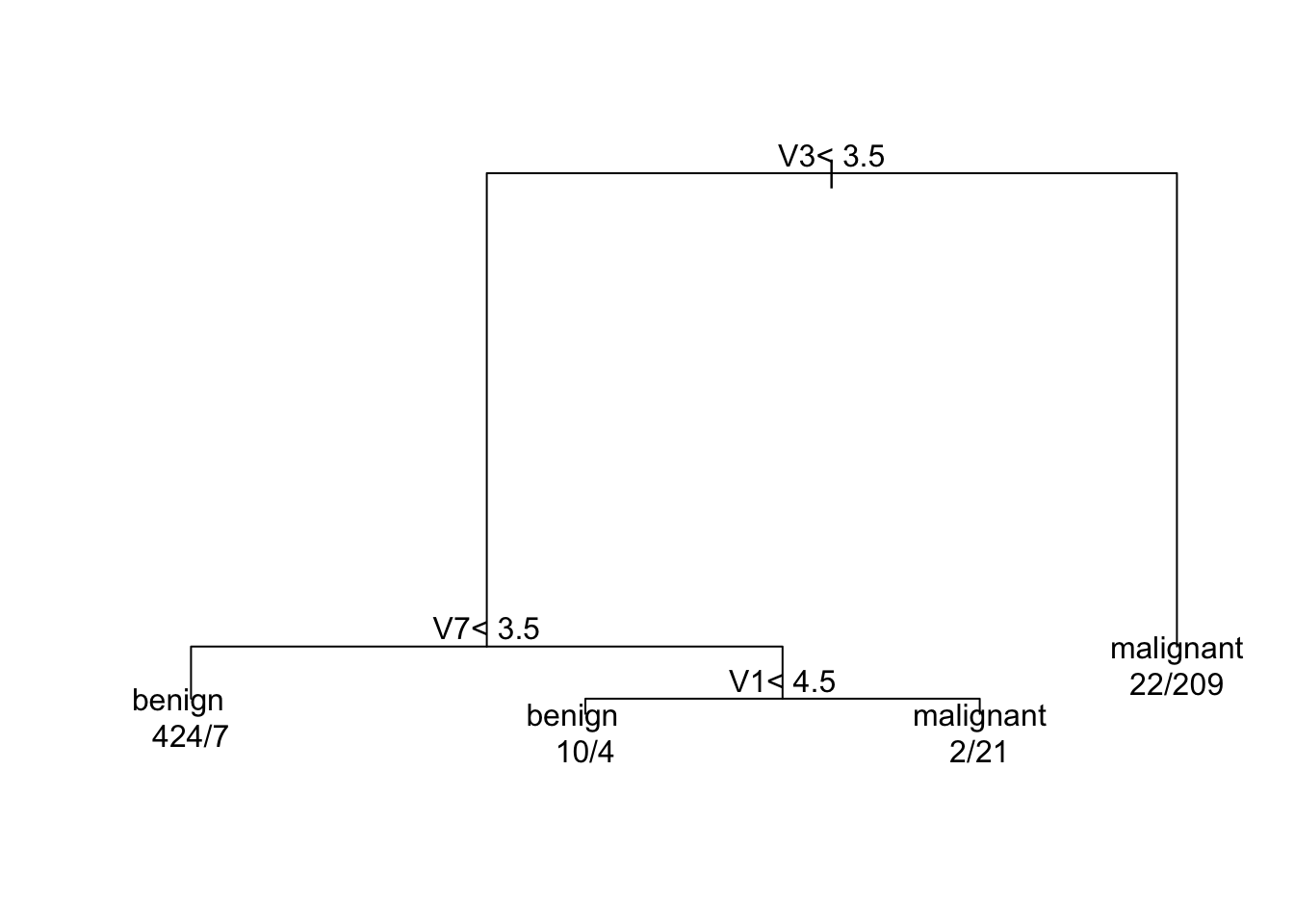
Fitted CART model for the biopsy data

Figure 6.1: Fitted CART model for the biopsy data

6.1.2 Out-of-sample comparisons

  • Looking at out-of-sample performance is a better way to validate our risk scores.

  • Let’s try a validation exercise by “training” our models on the first \(400\) observations of biopsy and then testing relative performance on the remaining observations.

# Create train/test splits for biopsy data
biopsy.train <- biopsy[1:400,]
biopsy.test <- biopsy[401:699,]
# Now, use each type of method on this training data
cart.model.train <- rpart(class ~ V1 + V3 + V4 + V7 + V8, data=biopsy.train)
logreg.model.train <- glm(tumor.type ~ V1 + V3 + V4 + V7 + V8, family="binomial", 
                    data=biopsy.train)
RF.model.train <- randomForest(class ~ V1 + V3 + V4 + V7 + V8, data=biopsy.train, 
                         ntree = 500)
  • Using these models built on the training data, get the fitted probabilities for the test data
risk.cart.test <- predict(cart.model.train, newdata=biopsy.test)[,2]
risk.logreg.test <- predict(logreg.model.train, newdata=biopsy.test, type="response")
risk.RF.test <- predict(RF.model.train, newdata=biopsy.test, type = "prob")[,2]
  • Now, using these fitted probabilities on the test data, compute the Brier scores:
brier.cart.test <- mean((risk.cart.test - biopsy.test$tumor.type)^2)
brier.logreg.test <- mean((risk.logreg.test - biopsy.test$tumor.type)^2)
brier.RF.test <- mean((risk.RF.test - biopsy.test$tumor.type)^2)

round(c(brier.cart.test, brier.logreg.test, brier.RF.test), 4)
## [1] 0.0359 0.0135 0.0190

  • For the out-of-sample Brier score, both logistic regression and random forest are notably better than CART.

  • Logistic regression is actually slightly better than random forest in out of sample performance with random forest (at least for this particular train/test split).

6.2 Brier Scores with Longitudinal Data

  • Let’s revisit the ohio data again from the geepack package
library(geepack)
data(ohio)
head(ohio, 10)
##    resp id age smoke
## 1     0  0  -2     0
## 2     0  0  -1     0
## 3     0  0   0     0
## 4     0  0   1     0
## 5     0  1  -2     0
## 6     0  1  -1     0
## 7     0  1   0     0
## 8     0  1   1     0
## 9     0  2  -2     0
## 10    0  2  -1     0

  • Each individual has 4 follow-up visits.

  • The variable resp is the wheezing status of the individual at each follow up.

  • The variable smoke is a baseline variable that does not change over time. This is an indicator of maternal smoking.

  • age is a time-varying covariate.

6.2.1 Option 1

  • If we want to build a risk score for wheezing, evaluating the performance of this risk score will depend on exactly what we are trying to predict.

  • Option 1: We want to predict whether or not some someone is diagnosed with wheezing over some time window, and we do not want to predict wheezing status at each time point.

  • As an example of this, let’s build a risk score which:

    • Only uses smoke as a covariate.

    • Builds the risk score from the first two follow-up times.

  • Let’s first construct a dataset called atleastone1 that records whether or not an individual had at least one positive wheezing status over the first two visits:
    • atleastone2 will record whether or not an individual has at least one positive wheezing status over the last two visits.
data(ohio)
baseline.ohio <- subset(ohio, age== -1) # data from baseline visit
firsttwo.ohio <- subset(ohio, age== -1 | age == 0) # data from visits 1-2
lasttwo.ohio <- subset(ohio, age==1 | age==2) # data from visits 3-4

tmp <- aggregate(firsttwo.ohio$resp, by=list(id=firsttwo.ohio$id), FUN=max)
tmp2 <- aggregate(lasttwo.ohio$resp, by=list(id=lasttwo.ohio$id), FUN=max)
atleastone1 <- merge(tmp, baseline.ohio, by="id")
atleastone2 <- merge(tmp2, baseline.ohio, by="id")
head(atleastone1)
##   id x resp age smoke
## 1  0 0    0  -1     0
## 2  1 0    0  -1     0
## 3  2 0    0  -1     0
## 4  3 0    0  -1     0
## 5  4 0    0  -1     0
## 6  5 0    0  -1     0
table(atleastone1$resp)
## 
##   0   1 
## 446  91
  • Let’s now build a risk score using only variable smoke as a covariate and a random choice of \(300\) observations
set.seed(1234)
train.ind <- sample(1:537, size=300)
atleastone1.train <- atleastone1[train.ind,]
mod1 <- glm(resp ~ smoke, family="binomial", data=atleastone1.train)
summary(mod1)
## 
## Call:
## glm(formula = resp ~ smoke, family = "binomial", data = atleastone1.train)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -0.5978  -0.5978  -0.5537  -0.5537   1.9754  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -1.7979     0.2078  -8.653   <2e-16 ***
## smoke         0.1665     0.3311   0.503    0.615    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 253.63  on 299  degrees of freedom
## Residual deviance: 253.37  on 298  degrees of freedom
## AIC: 257.37
## 
## Number of Fisher Scoring iterations: 4
  • The risk scores for the hold-out individuals for the later follow-up times are given by
risk1 <- predict(mod1, newdata=atleastone2[-train.ind,],
                 type="response")
  • Now, let’s look at the Brier score on the remaining individuals in the atleast2 data set.
mean((risk1 - atleastone2[-train.ind,]$resp)^2)
## [1] 0.1574466

  • An AUC probably does not make much sense here since there are only two possible values of the risk score.

  • For calibration, we can just compare the predicted risk scores and the mean number of successes in each of the smoking categories in the hold-out sample:

table(risk1)
## risk1
## 0.142105263157904 0.163636363636364 
##               160                77
table(atleastone2[-train.ind,]$resp, atleastone2[-train.ind,]$smoke)
##    
##       0   1
##   0 135  56
##   1  25  21
# Compare risk scores with 
25/(25 + 135)
## [1] 0.15625
21/(21 + 56)
## [1] 0.2727273
  • This risk score does not seem all that well-calibrated for later time points.
    • The overall prevalence of wheezing is a little bit higher in the hold-out sample.
    • There is a larger difference between the smoking and non-smoking groups in the hold-out sample.

6.2.2 Option 2

  • As another option, you may want to predict outcomes for each time point in the hold-out dataset.

  • In this case, I would probably just compute a Brier score by just averaging over all time points.

  • For example, with a GEE, you might do the following:

ind <- c(1:400, 801:1200, 1601:2000) ## index of training set
ohio.train <- subset(ohio[ind,], age==-1 | age == 0)
ohio.test <- subset(ohio[-ind,], age==1 | age==2)
fit.ex <- geeglm(resp ~ age + smoke + age:smoke, id=id, data=ohio.train,
                 family=binomial, corstr="exch")
rs2 <- predict(fit.ex, newdata=ohio.test, type="response")

## Now, find Brier score that the takes average across all individuals and time points
mean((rs2 - ohio.test$resp)^2)
## [1] 0.1270949