Chapter 1 Mixed Models for Longitudinal Data Analysis

1.1 Methods for Analyzing Longitudinal Data

  • Longitudinal data refers to data that:

    • Has multiple individuals.

    • Each individual has multiple observations over time.

  • We will denote the outcomes of interest with \(Y_{ij}\).

    • \(Y_{ij}\) - outcome for individual \(i\) at time \(t_{ij}\).

    • The \(i^{th}\) individual has \(n_{i}\) observations: \(Y_{i1}, \ldots, Y_{in_{i}}\).

    • There will be \(m\) individuals in the study (so \(1 \leq i \leq m\)).

    • \(\mathbf{x}_{ij} = (x_{ij1}, \ldots, x_{ijp})\) is the vector of covariates for individual \(i\) at time \(t_{ij}\).

    • Note that the vector \(\mathbf{x}_{ij}\) will often include the time point \(t_{ij}\) as a covariate.

  • Note: For your project, you may have to do some data processing of the data to get it into the form \((Y_{ij}, \mathbf{x}_{ij})\), for \(j = 1,\ldots,n_{i}\).

    • For example, although the data that you analyze for the project look at certain variables over time, they could be recorded “asynchronously” in some way.

    • This means meaning that the outcomes \(Y_{ij}\) and the covariates \(\mathbf{x}_{ij}\) are not exactly matched in time.

    • For example, on a given day, you may observe \(Y_{ij}\) at times 9:00, 10:00, and 11:00, but observe the covariate of interest at 9:17, 9:53, and 11:08.

    • Or, your outcome \(Y_{ij}\) may only be observed once per week, while the covariates of interest are measured multiple times per week.

    • We will discuss some ways of organizing asynchronous longitudinal data later in the class.

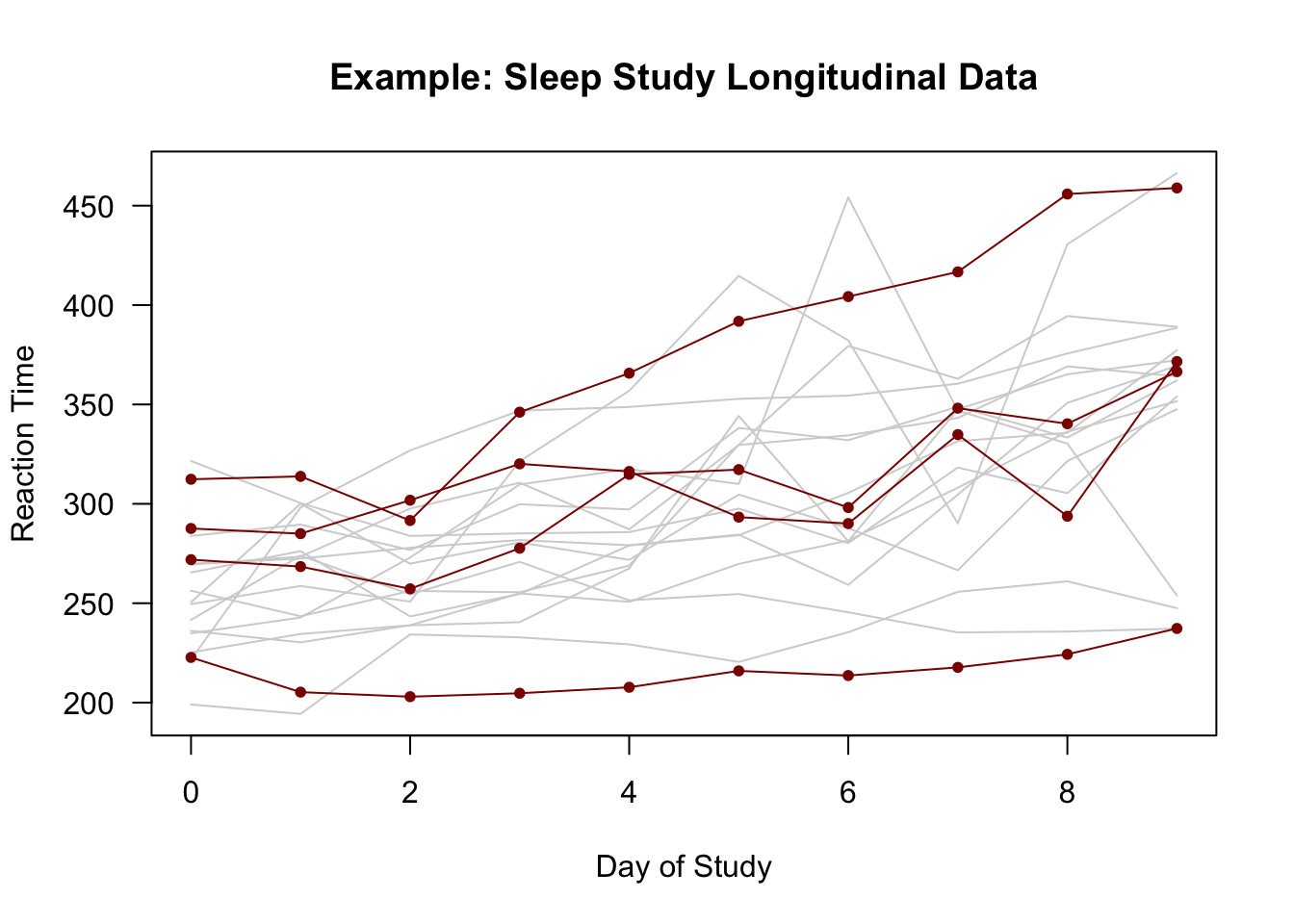
Plots of individual-specific trajectories from the sleepstudy data with the trajectories of 4 individuals highlighted.

Figure 1.1: Plots of individual-specific trajectories from the sleepstudy data with the trajectories of 4 individuals highlighted.

  • The above figure shows an example of outcomes from a longitudinal study (the sleepstudy data in the lme4 package).

  • In the sleepstudy data:

    • The observation time points of observation \(t_{ij}\) are the same for each individual \(i\). So, we can say \(t_{ij} = t_{j}\) for all \(i\).

    • The outcome \(Y_{ij}\) is the reaction time for the \(i^{th}\) individual at time point \(t_{j}\).

    • The 10 time points are \((t_{1}, \ldots, t_{10}) = (0, 1, \ldots, 9)\).

    • There are \(m = 18\) individuals in the study.

    • Each individual is observed at \(10\) time points. So, \(n_{i} = 10\) for every \(i\).

  • Most of the well-known regression-based methods for analyzing longitudinal data can be classified (see Diggle et al. (2013)) into one of the three following categories:
    • Random effects/mixed models,
    • Marginal models,
    • Transition models
  • Random effects/Mixed Models

    • “Random effects” are added to the regression model describing the outcomes for each individual.

    • These “random regression coefficients” are viewed as a sample from some distribution.

  • Marginal models

    • Regression coefficients have a “population average” interpretation.

    • Only mean of \(Y_{ij}\) and correlation structure of \((Y_{i1}, \ldots, Y_{in_{i}})\) are modeled.

    • Generalized estimating equations (GEEs) are often used for estimating model parameters.

  • Transition models
    • Choose a probability model for the distribution of \(Y_{ij}\) given the value of the outcome at the previous time point \(Y_{ij-1}\).

1.2 Mixed Models for Continuous Outcomes

  • If each \(Y_{ij}\) is a continuous outcome and we were to build a regression model without any random effects, we might assume something like: \[\begin{equation} Y_{ij} = \beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + e_{ij} \tag{1.1} \end{equation}\]

  • \(\mathbf{x}_{ij} = (x_{ij1}, \ldots, x_{ijp})\) is the vector of covariates for individual \(i\) at time \(t_{ij}\).

  • The vector \(\mathbf{x}_{ij}\) could contain individual information such as smoking status or age.

    • \(\mathbf{x}_{ij}\) could also contain some of the actual time points: \(t_{ij}, t_{ij-1}, ...\) or transformations of these time points.

  • The regression model (1.1) assumes the same mean function \(\beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta}\) holds for all individuals that have the same value of \(\mathbf{x}_{ij}\).

  • It is often reasonable to assume that the regression coefficients vary across individuals.

    • This can often better account for heterogeneity across individuals.

  • The figure below shows 3 different regression lines from the sleepstudy data.

    • Each regression line was estimated using only data from one individual.
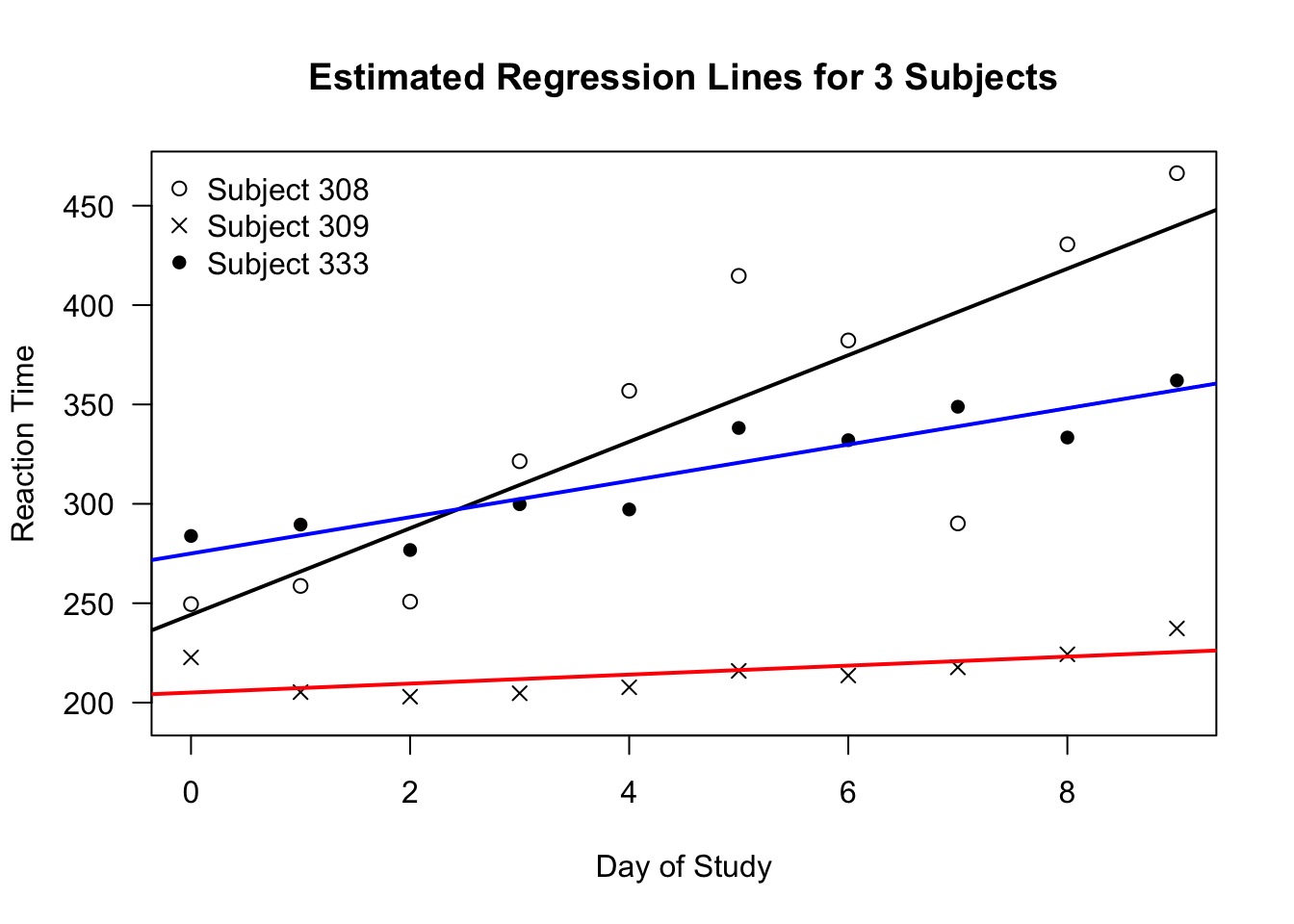
Separately estimated regression lines for 3 subjects in the sleepstudy data.

Figure 1.2: Separately estimated regression lines for 3 subjects in the sleepstudy data.

  • Figure 1.1 suggests there is some heterogeneity in the relationship between study day and response time across individuals.

  • The response time of Subject 309 changes very little over time.

  • For Subject 308, there is a more clear positive association between response time and day of study.

  • For the sleepstudy data, a linear regression for reaction time vs. study day which assumes that
    1. Expected response time is a linear function of study day,
    2. All individuals have the same regression coefficients,

would have the form: \[\begin{equation} Y_{ij} = \beta_{0} + \beta_{1} t_{j} + e_{ij} \end{equation}\]

  • If we allowed each individual to have his/her own intercept and slope, we could instead consider the following model \[\begin{equation} Y_{ij} = \beta_{0} + \beta_{1} t_{j} + u_{i0} + u_{i1}t_{j} + e_{ij} \tag{1.2} \end{equation}\]

  • \(\beta_{0} + u_{i0}\) - intercept for individual \(i\).

  • \(\beta_{1} + u_{i1}\) - slope for individual \(i\).

  • If we assume \((u_{i0}, u_{i1})\) are sampled from some distribution, \(u_{i0}\) and \(u_{i1}\) are referred to as random effects.

  • Typically, it is assumed that \((u_{i0}, u_{i1})\) are sampled from a multivariate normal distribution with mean zero: \[\begin{equation} (u_{i0}, u_{i1}) \sim \textrm{Normal}( \mathbf{0}, \boldsymbol{\Sigma}_{\tau} ) \end{equation}\]

  • Model (1.2) is called a mixed model because it contains both fixed effects \((\beta_{0}, \beta_{1})\) and random effects \((u_{i0}, u_{i1})\).

  • More generally, a linear mixed model (LMM) for longitudinal data will have the form: \[\begin{equation} Y_{ij} = \beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}\mathbf{u}_{i} + e_{ij} (\#eq:lmm-generalform) \end{equation}\]
    • \(\boldsymbol{\beta}\) - vector of fixed effects
    • \(\mathbf{u}_{i}\) - vector of random effects
  • If we stack the responses into a long vector \(\mathbf{Y}\) and random effects into a long vector \(\mathbf{u}\)
    • \(\mathbf{Y} = (Y_{11}, Y_{12}, ...., Y_{mn_{m}})\) - this vector has length \(\sum_{k=1}^{m} n_{k}\)
    • \(\mathbf{u} = (u_{10}, u_{11}, ...., u_{mq})\) - this vector has length \(m \times (q + 1)\).
  • Then, we can write the general form (??) of the LMM as \[\begin{equation} \mathbf{Y} = \mathbf{X}\tilde{\boldsymbol{\beta}} + \mathbf{Z}\mathbf{u} + \mathbf{e} \end{equation}\]
    • \(i^{th}\) row of \(\mathbf{X}\) is \((1, \mathbf{x}_{ij}^{T})\).
    • \(i^{th}\) row of \(\mathbf{Z}\) is \(\mathbf{z}_{ij}^{T}\).
    • \(\tilde{\boldsymbol{\beta}} = (\beta_{0}, \boldsymbol{\beta})\).
  • Constructing an LMM can be thought of as choosing the desired “\(\mathbf{X}\)” and “\(\mathbf{Z}\)” matrices.

1.3 Advantages of using random effects

1.3.1 Within-subject correlation

  • Using an LMM automatically accounts for the “within-subject” correlation.

    • That is, the correlation between two observations from the same individual.

  • This correlation arises because observations on the same individual “share” common random effects.

  • The correlation between the \(j^{th}\) and \(k^{th}\) observation from individual \(i\) is \[\begin{equation} \textrm{Corr}(Y_{ij}, Y_{ik}) = \frac{ \mathbf{z}_{ij}^{T}\boldsymbol{\Sigma}_{\tau}\mathbf{z}_{ik} }{ \sqrt{\sigma^{2} + \mathbf{z}_{ij}^{T}\boldsymbol{\Sigma}_{\tau}\mathbf{z}_{ij}}\sqrt{\sigma^{2} + \mathbf{z}_{ik}^{T}\boldsymbol{\Sigma}_{\tau}\mathbf{z}_{ik}}} \end{equation}\]

  • When using only a random intercept, the correlation between \(Y_{ij}\) and \(Y_{ik}\) is \[\begin{equation} \textrm{Corr}(Y_{ij}, Y_{ik}) = \frac{ \sigma_{u}^{2} }{ \sigma^{2} + \sigma_{u}^{2} } \end{equation}\]
    • In this case, \(\mathbf{z}_{ij} = 1\) and \(u_{i} \sim \textrm{Normal}(0, \sigma_{u}^{2})\)
    • \(\sigma^{2}\) is the variance of the residual term \(e_{ij}\)
  • For longitudinal data, one criticism of the random intercept model is that the within-subject correlation does not vary across time.

1.3.2 Inference about Heterogeneity - Variance of Random Effects

  • One of the goals of the data analysis may be to characterize the heterogeneity in the relationship between the outcome and some of the covariates across individuals.

  • Looking at the estimates of the variance of the random effects is one way of addressing this goal.

  • An estimate of \(\textrm{Var}( u_{ih} )\) “substantially greater than zero” is an indication that there is variability in the regression coefficient corresponding to \(u_{ih}\) across individuals.

  • For example, with the random intercept and slope model for the sleepstudy data \[\begin{equation} Y_{ij} = \beta_{0} + \beta_{1}t_{j} + u_{i0} + u_{i1}t_{j} + e_{ij} \end{equation}\]

  • If \(\textrm{Var}( u_{i1} )\) is “large”, this implies that the response to additional days of sleep deprivation varies considerably across individuals.

    • The response time of some individuals is not impacted much by additional days of little sleep.

    • Some individuals respond strongly to additional days of little sleep.

1.3.3 Best Linear Unbiased Prediction

  • You may want to estimate or “predict” the mean function/trajectory of a given individual.

  • This means you want to estimate/predict the following quantity: \[\begin{equation} \beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}\mathbf{u}_{i} \end{equation}\]

  • The “Best Linear Unbiased Predictor” (BLUP) of this is \[\begin{equation} \textrm{BLUP}(\beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}\mathbf{u}_{i}) = \beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}E(\mathbf{u}_{i}|Y_{i1}, \ldots, Y_{in_{i}}) \end{equation}\]

  • I would think of the values of \(\textrm{BLUP}(\beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}\mathbf{u}_{i})\) (for different values of \(j\)) as an estimate of the “true trajectory” (i.e., the true mean) of the \(i^{th}\) individual.

  • The observed longitudinal outcomes from individual \(i\) are a “noisy estimate” of that individual’s true trajectory.

  • The BLUPs are more stable “shrinkage” estimates of the trajectory of individual \(i\).

    • These are called shrinkage estimates because often shrinks the estimate that would be obtained using only data from individual \(i\) towards the “overall” estimate \(\mathbf{x}_{ij}^{T}\boldsymbol{\beta}\).

  • For example, if we had the intercept-only model \(Y_{ij} = \beta_{0} + u_{i} + e_{ij}\), the value of the BLUPs is \[\begin{equation} \textrm{BLUP}(\beta_{0} + u_{i}) = \frac{n_{i}\sigma_{u}^{2}}{\sigma^{2} + n_{i}\sigma_{u}^{2} }\bar{Y}_{i.} + \Big(1 - \frac{n_{i}\sigma_{u}^{2}}{\sigma^{2} + n_{i}\sigma_{u}^{2} }\Big)\bar{Y}_{..} \end{equation}\]

  • \(\bar{Y}_{i.}\) is the sample mean from individual-\(i\) data

    • \(\bar{Y}_{i.}\) would be the estimate of the intercept if we only looked at data from the \(i^{th}\) individual.

  • \(\bar{Y}_{..}\) - overall mean

    • \(\bar{Y}_{..}\) would be the estimate of the intercept if we ignored variation in intercepts across individuals.

  • You can also think of \(\textrm{BLUP}(\beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}\mathbf{u}_{i})\) as a prediction of what the observed trajectory for individual \(i\) would be if that individual were in a future study under the same conditions.

  • Say \(Y_{i1}', \ldots, Y_{in_{i}}'\) are the observations for individual \(i\) in a future study.

  • The outcomes in the future study are determined by \[\begin{equation} Y_{ij}' = \beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}\mathbf{u}_{i} + e_{ij}' \end{equation}\]

  • The expectation of \(Y_{ij}'\) given the observed data in our longitudinal study is \[\begin{eqnarray} E(Y_{ij}'|Y_{i1}, \ldots, Y_{in_{i}}) &=& \beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}E(\mathbf{u}_{i}|Y_{i1}, \ldots, Y_{in_{i}}) \nonumber \\ &=& \textrm{BLUP}(\beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}\mathbf{u}_{i}) \nonumber \end{eqnarray}\]

1.4 Generalized linear mixed models (GLMMs)

  • Generalized linear models (GLMs) are used to handle data (often “non-continuous”) that can’t be reasonably modeled with a Gaussian distribution.

  • The most common scenarios where you would use GLMs in practice are binary, count, and multinomial outcomes.

  • With a generalized linear mixed model (GLMM), you assume that a GLM holds conditional on the value of the random effects.

1.4.1 GLMMs with Binary Outcomes

  • Under the GLM framework, the usual approach for handling binary outcomes is logistic regression.

  • The assumptions underlying logistic regression are:

    • The outcomes are independent

    • Each outcome follows a Bernoulli distribution.

    • The log-odds parameter is assumed to be a linear combination of the covariates.

  • With the GLMM version of logistic regression, we will make almost the same assumptions as the regular GLM version of logistic regression.
    • The main difference is that each assumption in the GLMM will be conditional on the values of the random effects.
  • To be specific, for longitudinal binary outcomes \(Y_{ij}\), the GLMM version of logistic regression assumes the following:

    1. Conditional on the vector of random effects \(\mathbf{u}_{i}\) \[\begin{equation} Y_{i1}, \ldots, Y_{in_{i}}|\mathbf{u}_{i} \textrm{ are independent } \end{equation}\]

    2. Conditional on \(\mathbf{u}_{i}\), each \(Y_{ij}\) has a Bernoulli distribution \[\begin{equation} Y_{ij}|\mathbf{u}_{i} \sim \textrm{Bernoulli}\big\{ p_{ij}(\mathbf{u}_{i}) \big\} \end{equation}\] so that \(p_{ij}( \mathbf{u}_{i} ) = P(Y_{ij} = 1| \mathbf{u}_{i})\).

    3. The “conditional” log-odds term \(\log\{ p_{ij}(\mathbf{u}_{i})/[1 - p_{ij}(\mathbf{u}_{i})] \}\) is a linear combination of the covariates and the random effects vector \(\mathbf{u}_{i}\): \[\begin{equation} \textrm{logit}\{ p_{ij}(\mathbf{u}_{i}) \} = \log\Big( \frac{ p_{ij}(\mathbf{u}_{i})}{ 1 - p_{ij}(\mathbf{u}_{i}) } \Big) = \beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}\mathbf{u}_{i} \end{equation}\]

    4. As with a linear mixed model, we assume that the random-effects vector \(\mathbf{u}_{i}\) has a multivariate normal distribution with mean zero and covariance matrix \(\boldsymbol{\Sigma}_{\tau}\) \[\begin{equation} \mathbf{u}_{i} \sim \textrm{Normal}( \mathbf{0}, \boldsymbol{\Sigma}_{\tau}) \end{equation}\]

1.4.2 GLMMs with Count Outcomes

  • For count outcomes, responses are typically assumed to follow a Poisson distribution and sometimes a negative binomial distribution - conditional on the values of the random effects.

  • For the Poisson model, we assume \(Y_{ij}|\mathbf{u}_{i} \sim \textrm{Poisson}\{ \mu_{ij}( \mathbf{u}_{i} ) \}\), \[\begin{equation} E(Y_{ij}| \mathbf{u}_{i}) = \mu_{ij}(\mathbf{u}_{i}) \qquad \textrm{Var}( Y_{ij}| \mathbf{u}_{i} ) = \mu_{ij}(\mathbf{u}_{i}) \end{equation}\]

  • One common problem with the Poisson distribution is overdispersion (i.e., variance is greater than the mean).

    • The variance of the Poisson equals the mean.

    • While the marginal variance will not equal the mean in a GLMM, requiring the conditional means and variances to be equal could lead to a poor fit.

  • For the negative binomial model, we assume
    \(Y_{ij}|\mathbf{u}_{i} \sim \textrm{NB}\{ \mu_{ij}( \mathbf{u}_{i}) , \phi \}\), \[\begin{equation} E(Y_{ij}| \mathbf{u}_{i}) = \mu_{ij}(\mathbf{u}_{i}) \qquad \textrm{Var}( Y_{ij}| \mathbf{u}_{i} ) = \mu_{ij}(\mathbf{u}_{i}) + \phi\mu_{ij}^{2}(\mathbf{u}_{i}) \end{equation}\]

    • \(\phi\) is often referred to as the overdispersion parameter.

  • With a GLMM model for count data, it is typical to model the log of the conditional mean \(\mu_{ij}(\mathbf{u}_{i})\) with a linear regression: \[\begin{equation} \log\{ \mu_{ij}(\mathbf{u}_{i}) \} = \beta_{0} + \mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}^{T}\mathbf{u}_{i} \end{equation}\]

  • Again, for the Poisson GLMM, the usual assumption for the random effects is that \[\begin{equation} \mathbf{u}_{i} \sim \textrm{Normal}( \mathbf{0}, \boldsymbol{\Sigma}_{\tau}) \end{equation}\]

1.5 Fitting Linear Mixed Models (LMMs) and Generalized Linear Mixed models (GLMMs) in R

  • The lme4 package is probably the most general package for fitting LMMs and GLMMs.
library(lme4)
  • With Python, you can use the mixedlm function from the statmodels module to fit linear mixed models.

1.5.1 Fitting LMMs with the sleepstudy data

  • To start off, let’s use the sleepstudy longitudinal data in lme4 and look at the data from the first two individuals in this data.
data(sleepstudy) 
dim(sleepstudy) # 18 individuals, each with 10 observations
## [1] 180   3
sleepstudy[1:20,] # Data from the subjects with ids: 308 and 309
##    Reaction Days Subject
## 1  249.5600    0     308
## 2  258.7047    1     308
## 3  250.8006    2     308
## 4  321.4398    3     308
## 5  356.8519    4     308
## 6  414.6901    5     308
## 7  382.2038    6     308
## 8  290.1486    7     308
## 9  430.5853    8     308
## 10 466.3535    9     308
## 11 222.7339    0     309
## 12 205.2658    1     309
## 13 202.9778    2     309
## 14 204.7070    3     309
## 15 207.7161    4     309
## 16 215.9618    5     309
## 17 213.6303    6     309
## 18 217.7272    7     309
## 19 224.2957    8     309
## 20 237.3142    9     309
  • The sleepstudy data is an example of longitudinal data stored in long format (as opposed to “wide” format).
    • In long format, each row of the dataset corresponds to an observation from one individual at one time point.

  • The lmer function in lme4 fits linear mixed models.

    • This has many of the same features as the lm function in R.

  • To fit an LMM with lmer, the main thing to do is to specify the “X” part of the model (i.e., the fixed effects) and the “Z” part of the model (i.e., the random effects).

  • The “X” part of the model is done using the exact same “formula notation” used in the lm function.

  • The “Z” part of the model is done using the following type of syntax:

(formula | group_var)
  • group_var is the “grouping variable” used for the random effects

    • For longitudinal data, this would be the variable which identifies each individual.

    • For example, this might be an identifier variable which stores a separate id for each person.

1.5.1.1 LMM with a single, random intercept for each subject

  • Let’s fit an LMM where there is a fixed slope for time and only a random intercept for each Subject \[\begin{equation} Y_{ij} = \beta_{0} + \beta_{1}t_{j} + u_{i} + e_{ij} \tag{1.3} \end{equation}\]

  • For the “X” part of this model, we use Reaction ~ Days.

    • This gives us a fixed intercept and a fixed slope for the Days variable.

  • For the “Z” part of this model, we just add (1|Subject).

    • This says that there is only a random intercept within the grouping variable Subject.

  • Putting these two together, we can fit the LMM (1.3) using the following code:

lmm.sleep.intercept <- lmer(Reaction ~ Days + (1|Subject), data = sleepstudy)

  • You can always use the model.matrix method on the fitted lmer object to check that the “X” and “Z” matrices correspond to the model you want.

  • Let’s look at the first 5 rows of the “X” matrix from lmm.sleep.intercept

x.mat <- model.matrix(lmm.sleep.intercept)
## This design matrix should have an intercept column
## and a column which stores the "Days" variable
x.mat[1:5,]
##   (Intercept) Days
## 1           1    0
## 2           1    1
## 3           1    2
## 4           1    3
## 5           1    4
  • Let’s look at the first 20 rows of the “Z” matrix from lmm.intercept
## Use argument type = "random" to get random-effects design matrix
z.mat <- model.matrix(lmm.sleep.intercept, type="random")
z.mat[1:20,] # The . values in zmat correspond to zeros
## 20 x 18 sparse Matrix of class "dgCMatrix"
##   [[ suppressing 18 column names '308', '309', '310' ... ]]
##                                       
## 1  1 . . . . . . . . . . . . . . . . .
## 2  1 . . . . . . . . . . . . . . . . .
## 3  1 . . . . . . . . . . . . . . . . .
## 4  1 . . . . . . . . . . . . . . . . .
## 5  1 . . . . . . . . . . . . . . . . .
## 6  1 . . . . . . . . . . . . . . . . .
## 7  1 . . . . . . . . . . . . . . . . .
## 8  1 . . . . . . . . . . . . . . . . .
## 9  1 . . . . . . . . . . . . . . . . .
## 10 1 . . . . . . . . . . . . . . . . .
## 11 . 1 . . . . . . . . . . . . . . . .
## 12 . 1 . . . . . . . . . . . . . . . .
## 13 . 1 . . . . . . . . . . . . . . . .
## 14 . 1 . . . . . . . . . . . . . . . .
## 15 . 1 . . . . . . . . . . . . . . . .
## 16 . 1 . . . . . . . . . . . . . . . .
## 17 . 1 . . . . . . . . . . . . . . . .
## 18 . 1 . . . . . . . . . . . . . . . .
## 19 . 1 . . . . . . . . . . . . . . . .
## 20 . 1 . . . . . . . . . . . . . . . .

  • The . values in z.mat are just zeros.

  • Notice that each Subject has its own “intercept” column.

    • This what we want - each Subject has its own intercept.
  • Let’s look at the estimated parameters from the LMM with random intercepts using summary
summary(lmm.sleep.intercept)
## Linear mixed model fit by REML ['lmerMod']
## Formula: Reaction ~ Days + (1 | Subject)
##    Data: sleepstudy
## 
## REML criterion at convergence: 1786.5
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.2257 -0.5529  0.0109  0.5188  4.2506 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  Subject  (Intercept) 1378.2   37.12   
##  Residual              960.5   30.99   
## Number of obs: 180, groups:  Subject, 18
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept) 251.4051     9.7467   25.79
## Days         10.4673     0.8042   13.02
## 
## Correlation of Fixed Effects:
##      (Intr)
## Days -0.371

  • The estimated fixed-effects intercept is \(\hat{\beta}_{0} = 251.4\), and the estimated fixed-effects slope is \(\hat{\beta}_{1} = 10.5\).

  • The estimated variance of the random intercept is \(\hat{\tau}^{2} = 1378.2\) (standard deviation is \(\hat{\tau} = 37.1\)).

    • i.e., it is estimated that \(u_{i} \sim \textrm{Normal}(0, 1378.2)\).

1.5.1.2 LMM with both a random intercept and slope for each subject

  • Now, let’s fit an LMM where there is a fixed slope for time and both a random intercept and slope for each Subject \[\begin{equation} Y_{ij} = \beta_{0} + \beta_{1}t_{j} + u_{i0} + u_{i1}t_{j} + e_{ij} (\#eq:lmm-slope-sleep) \end{equation}\]

  • This is done with lmer using the following code:

lmm.sleep.slope <- lmer(Reaction ~ Days + (Days|Subject), data = sleepstudy)
  • Again, let’s check the “X” and “Z” matrices from lmm.sleep.slope to double-check that everything makes sense
x.mat2 <- model.matrix(lmm.sleep.slope)
## This design matrix should be the same as that from lmm.sleep.intercept
x.mat2[1:5,]
##   (Intercept) Days
## 1           1    0
## 2           1    1
## 3           1    2
## 4           1    3
## 5           1    4
  • First 20 rows of the “Z” matrix from lmm.sleep.slope:
## Use argument type = "random" to get random-effects design matrix
z.mat2 <- model.matrix(lmm.sleep.slope, type="random")
z.mat2[1:20,] # The . values in zmat2 correspond to zeros
## 20 x 36 sparse Matrix of class "dgCMatrix"
##   [[ suppressing 36 column names '308', '308', '309' ... ]]
##                                                                           
## 1  1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 2  1 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 3  1 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 4  1 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 5  1 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 6  1 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 7  1 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 8  1 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 9  1 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 10 1 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 11 . . 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 12 . . 1 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 13 . . 1 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 14 . . 1 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 15 . . 1 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 16 . . 1 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 17 . . 1 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 18 . . 1 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 19 . . 1 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
## 20 . . 1 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
  • Note that the two columns for each Subject in z.mat2 are of the form \((1, t_{j})\), which is what we want.
  • Let’s look at the estimated parameters from lmm.sleep.slope
summary(lmm.sleep.slope)
## Linear mixed model fit by REML ['lmerMod']
## Formula: Reaction ~ Days + (Days | Subject)
##    Data: sleepstudy
## 
## REML criterion at convergence: 1743.6
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.9536 -0.4634  0.0231  0.4634  5.1793 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  Subject  (Intercept) 612.10   24.741       
##           Days         35.07    5.922   0.07
##  Residual             654.94   25.592       
## Number of obs: 180, groups:  Subject, 18
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  251.405      6.825  36.838
## Days          10.467      1.546   6.771
## 
## Correlation of Fixed Effects:
##      (Intr)
## Days -0.138

  • The estimated fixed-effects coefficients are \(\hat{\beta}_{0} = 251.4\), and \(\hat{\beta}_{1} = 10.5\) respectively.

  • The estimated standard deviation and correlation of the random effects are

    • Estimated standard deviation of \(u_{i0}\) is \(24.7\).

    • Estimated standard deviation of \(u_{i1}\) is \(5.9\).

    • Estimated correlation between \(u_{i0}\) and \(u_{i1}\) is \(0.07\).

  • Rather than always printing out the entire summary, you can directly extract the estimates of the fixed effects with coef:
coef( summary(lmm.sleep.slope) )
##              Estimate Std. Error   t value
## (Intercept) 251.40510   6.824597 36.838090
## Days         10.46729   1.545790  6.771481
  • To directly extract the estimates of the variance (or standard deviation) of the random effects, you can use:
VarCorr( lmm.sleep.slope )
##  Groups   Name        Std.Dev. Corr 
##  Subject  (Intercept) 24.7407       
##           Days         5.9221  0.066
##  Residual             25.5918

Interpreting the estimated variance of the random effects

  • One way to think about the magnitude of the variance components is to look at the 5th and 95th percentiles of the random effects distribution.

    • For example, if you only have a random intercept term, then roughly \(90\%\) of individuals will have an intercept that falls in the interval \([\hat{\beta}_{0} - 1.64\hat{\sigma}_{u0}, \hat{\beta}_{0} + 1.64\hat{\sigma}_{u0}]\).

    • If you have a random slope term, then roughly \(90\%\) of individuals will have an intercept that falls in the interval \([\hat{\beta}_{1} - 1.64\hat{\sigma}_{u1}, \hat{\beta}_{1} + 1.64\hat{\sigma}_{u1}]\).

  • Another idea for helping to interpret the magnitude of the random effects is to plot many random trajectories for specific choices of the covariate vector \(\mathbf{x}_{i}\) (if the \(\mathbf{x}_{i}\) vary across individuals).
    • For example, in the sleepstudy data, you could plot \(\hat{\beta}_{0} + u_{i0} + \hat{\beta}_{1}t_{j} + u_{i1}t_{j}\) where the pairs \((u_{i0}, u_{i1})\) are generated from the estimated joint Normal distribution.
Sigma.hat <- VarCorr( lmm.sleep.slope )$Subject # This is the random-effects 
                                                # covariance matrix
ndraws <- 100
Sigma.hat.sqrt <- chol(Sigma.hat)
beta.hat <- coef( summary(lmm.sleep.slope) )[,1]  # estimated fixed effects
print(beta.hat)
## (Intercept)        Days 
##   251.40510    10.46729
plot(sleepstudy$Days, sleepstudy$Reaction, type="n", xlab="Days", ylab="Response", 
     las=1, main="sleepstudy: Variation in subject-specific trajectories")
for(k in 1:ndraws) {
   uvec.draw <- Sigma.hat.sqrt%*%rnorm(2)  # draw random (ui0, ui1) pair
   trajectory <- beta.hat[1] + uvec.draw[1] + (0:9)*(beta.hat[2] + uvec.draw[2])
   lines(0:9, trajectory)
}
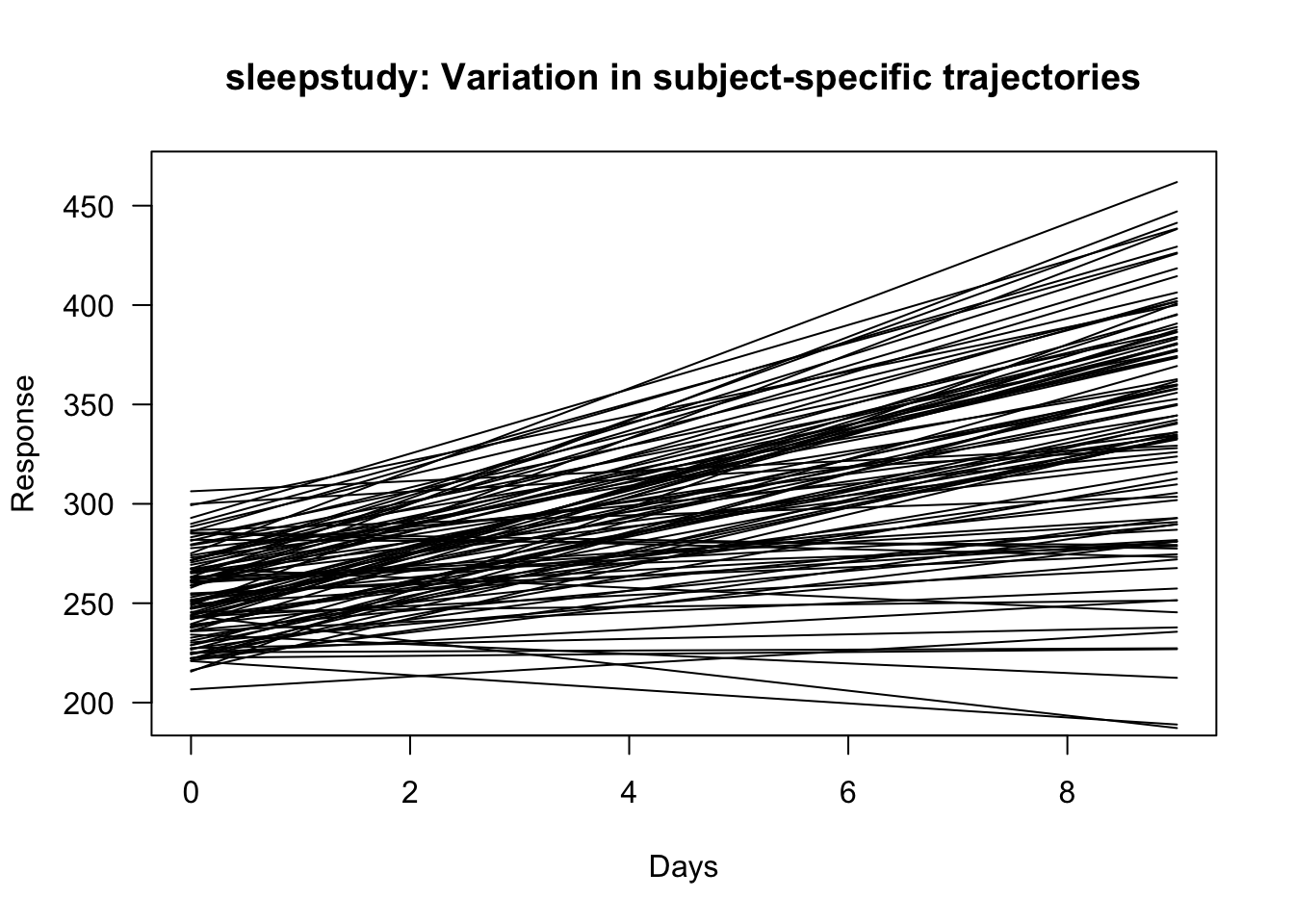
Random trajectories for sleepstudy data using the estimated intercept and slope random-effects variances.

Figure 1.3: Random trajectories for sleepstudy data using the estimated intercept and slope random-effects variances.

1.5.2 Model Comparison of LMMs using anova

  • The anova function can directly compare nested linear mixed models that are fit by lmer.
    • That is, where one larger model contains all of the components of the smaller model.
  • To use anova, you should include the argument REML = FALSE so lmer uses maximum likelihood estimation.
  • As an example, let’s compare the following two models on the sleelpstudy data
    • Model M0: Only has an intercept as a fixed effect and a random intercept for each person.
    • Model M1: Has an intercept and slope as the fixed effects and a random intercept for each person.
  • Let’s first fit these models using REML = FALSE:
M0 <- lmer(Reaction ~ 1 + (1|Subject), data = sleepstudy, REML=FALSE)
M1 <- lmer(Reaction ~ Days + (1|Subject), data = sleepstudy, REML=FALSE)
  • Running anova(M0, M1) will perform a chi-square test comparing these two models.
    • anova(M0, M1) also reports an AIC and BIC measure.
anova(M0, M1)
## Data: sleepstudy
## Models:
## M0: Reaction ~ 1 + (1 | Subject)
## M1: Reaction ~ Days + (1 | Subject)
##    npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## M0    3 1916.5 1926.1 -955.27   1910.5                         
## M1    4 1802.1 1814.8 -897.04   1794.1 116.46  1  < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  • We can see that the chi-square statistic is very large.
    • There is strong evidence in favor of model M1 over M0.
  • Now, suppose we want to compare the following two models
    • Model M1: Has an intercept and slope as the fixed effects and a random intercept for each person.
    • Model M2: Has an intercept and slope as the fixed effects and a random intercept and slope for each person.
  • To compare M1 with M2, let’s fit M2 with REML = FALSE:
M2 <- lmer(Reaction ~ Days + (Days|Subject), data = sleepstudy, REML=FALSE)
  • Now, use anova(M1, M2) to compare these models directly
anova(M1, M2)
## Data: sleepstudy
## Models:
## M1: Reaction ~ Days + (1 | Subject)
## M2: Reaction ~ Days + (Days | Subject)
##    npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## M1    4 1802.1 1814.8 -897.04   1794.1                         
## M2    6 1763.9 1783.1 -875.97   1751.9 42.139  2  7.072e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  • Based on the chi-square statistic and associated p-value, there is strong evidence favoring M2 over M1.

1.5.3 Extracting BLUPs in lme4

  • To get the “BLUPs” the intercepts and slopes \(\textrm{BLUP}(u_{i0})\) and \(\textrm{BLUP}(u_{i1})\), use ranef
blups.slope <- ranef( lmm.sleep.slope )
  • To plot these, use dotplot (you will need to load the lattice package first)
library(lattice)
dotplot(blups.slope)
## $Subject

## This plots subjects sorted by individual-specific estimates of intercepts
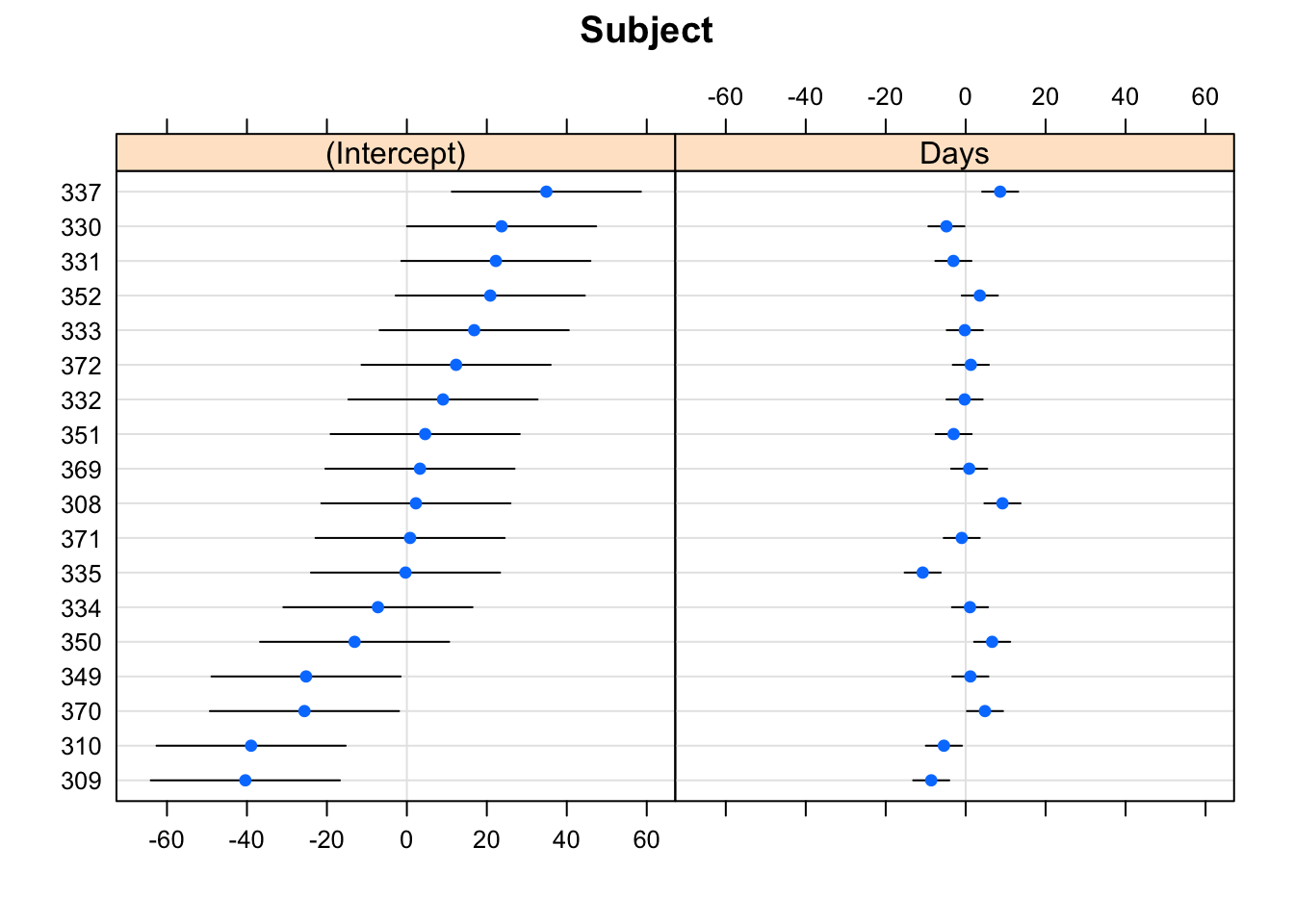
  • To extract the “predicted” random effects into a DataFrame use
ranef.df <- as.data.frame( blups.slope)
head(ranef.df)
##    grpvar        term grp    condval   condsd
## 1 Subject (Intercept) 308   2.258551 12.07086
## 2 Subject (Intercept) 309 -40.398738 12.07086
## 3 Subject (Intercept) 310 -38.960409 12.07086
## 4 Subject (Intercept) 330  23.690620 12.07086
## 5 Subject (Intercept) 331  22.260313 12.07086
## 6 Subject (Intercept) 332   9.039568 12.07086
  • This returns a data frame of the BLUPs for each random effect along with a “standard error” for each BLUP.

  • What we discussed earlier in Section 1.3, were the BLUPs for \(\mathbf{x}_{ij}^{T}\boldsymbol{\beta} + \mathbf{z}_{ij}\mathbf{u}_{i}\) not just the individual components of \(\mathbf{u}_{i}\).

  • For this random intercept and slope model, this is \(\textrm{BLUP}(\beta_{0} + \beta_{1}t_{j} + u_{i0} + u_{i1}t_{j})\)

  • These are obtained by using the fitted method

blup.full <- fitted( lmm.sleep.slope )  # Should be a vector of length 180
  • If we plot \(\textrm{BLUP}(\beta_{0} + \beta_{1}t_{j} + u_{i0} + u_{i1}t_{j})\) as a function of time for all individuals, it will look like the following:
library(ggplot2)
# First add the BLUPs to the sleepstudy data as a separate variable
sleepstudy$blups <- blup.full

# Now plot BLUPs vs. study data for each subject
ggplot(sleepstudy, aes(x=Days, y=blups, group=Subject)) +
  geom_line(aes(color=Subject)) + 
  labs(title = "BLUPs in Random Intercept + Random Slope Model",
       y = "Reaction Time")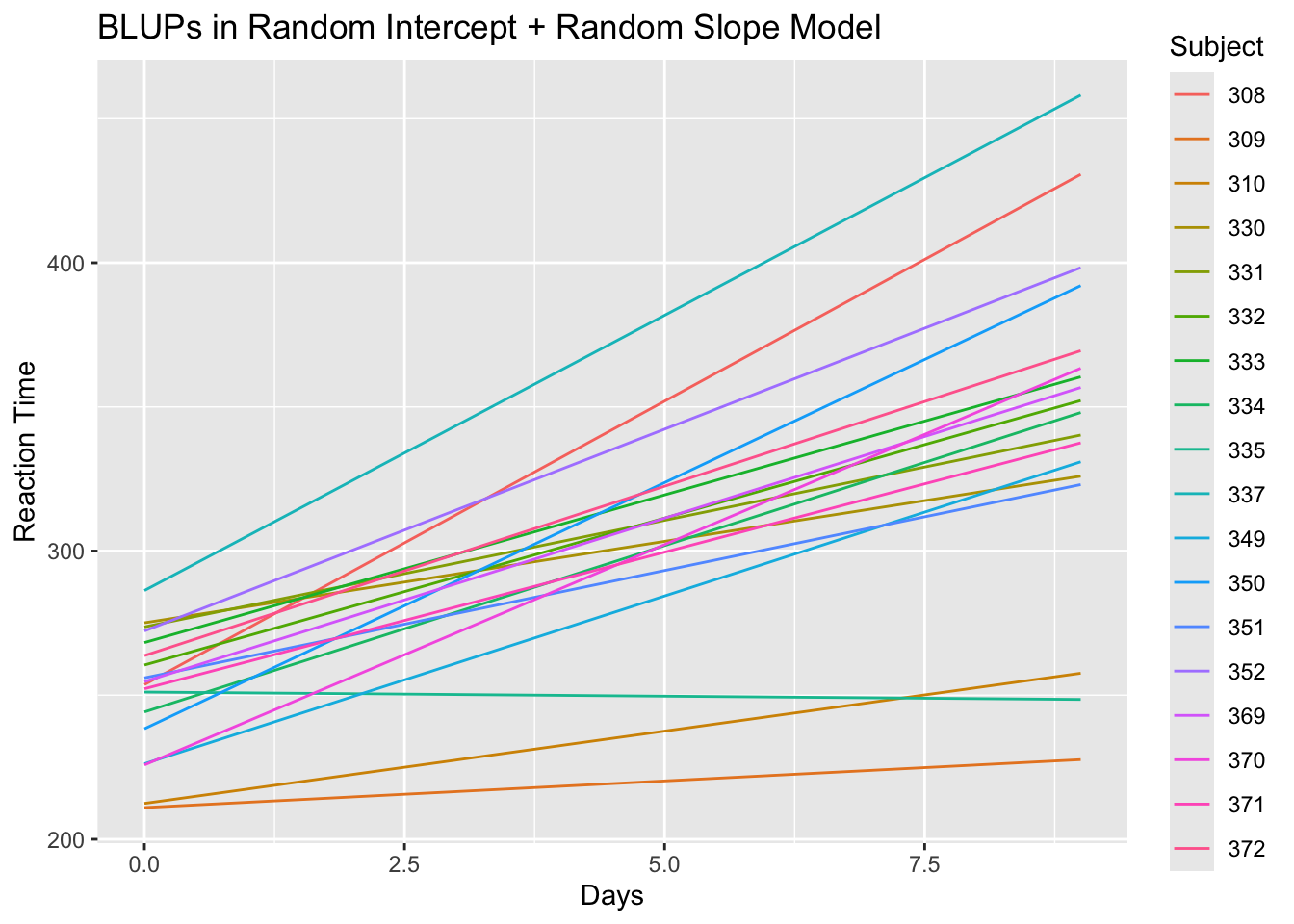

1.5.4 Fitting Binary GLMMs using the Ohio data

  • To use the ohio data, we will first load the geepack R package:
library(geepack)
  • This dataset has 2148 observations from 537 individuals
data(ohio)
head(ohio, 12) # look at first 12 rows of ohio
##    resp id age smoke
## 1     0  0  -2     0
## 2     0  0  -1     0
## 3     0  0   0     0
## 4     0  0   1     0
## 5     0  1  -2     0
## 6     0  1  -1     0
## 7     0  1   0     0
## 8     0  1   1     0
## 9     0  2  -2     0
## 10    0  2  -1     0
## 11    0  2   0     0
## 12    0  2   1     0

  • The outcome of interest in ohio is “wheezing status”: 1 - yes, 0 - no.

    • The resp variable contains wheezing status.

  • The id variable contains the unique identifier for each individual.

  • The age in the ohio dataset is the time variable.

    • The age variable is recorded as: (age in years - 9).

    • Each individual starts the study at 7 years of age.

  • The smoke variable is an indicator of maternal smoking at the starting year of the study.

  • In lme4, fitting a GLMM with binary responses can be done with the glmer function.

  • The glmer function has the following syntax:

glmer(formula, data, family)

  • The formula argument uses the same syntax as lmer

  • When handling binary outcomes, you need to specify the family argument as: family = binomial.

  • Just exploring this data by looking at the raw proportions, it appears that
    • probability of wheezing decreases as age increases (within each level of smoking)
    • maternal smoking increases the probability of wheezing at each age
library(dplyr)
prop_summary_ohio <- ohio %>% 
                     group_by(smoke, age) %>% 
                     summarize( prop_wheeze = mean(resp) )
prop_summary_ohio
## # A tibble: 8 × 3
## # Groups:   smoke [2]
##   smoke   age prop_wheeze
##   <int> <int>       <dbl>
## 1     0    -2       0.16 
## 2     0    -1       0.149
## 3     0     0       0.143
## 4     0     1       0.106
## 5     1    -2       0.166
## 6     1    -1       0.209
## 7     1     0       0.187
## 8     1     1       0.139
  • So, we are probably going to want to include both age and smoke in our model.

1.5.4.1 A Random Intercept Model

  • Let’s use a GLMM to explore the relationship between wheezing status and the:
    • age of the child
    • maternal smoking status
  • A GLMM for wheezing status which has age and smoking status as fixed effects and random individual-specific intercepts can be expressed as
\[\begin{equation} \textrm{logit}\{ p_{ij}(u_{i}) \} = \beta_{0} + \beta_{age}\textrm{age}_{ij} + \beta_{smk}\textrm{smoke}_{i} + u_{i} \tag{1.4} \end{equation}\]
  • Model (1.4) can be fit with the following code
# id is the grouping variable
ohio.intercept <- glmer(resp ~ age + smoke + (1 | id), data = ohio, family = binomial)
coef(summary(ohio.intercept))
##               Estimate Std. Error    z value     Pr(>|z|)
## (Intercept) -3.3739539 0.27497502 -12.270038 1.311914e-34
## age         -0.1767645 0.06796698  -2.600741 9.302258e-03
## smoke        0.4147806 0.28704052   1.445024 1.484510e-01
VarCorr(ohio.intercept)
##  Groups Name        Std.Dev.
##  id     (Intercept) 2.3432

  • For a binary GLMM, the estimated standard deviation for the random intercept can be a little hard to interpret, though this value seems rather large to me.

  • One way to report this is to look at the variation in \(p_{ij}(u_{i})\) for different values of age and smoking status.

    • For this purpose, you could report the interval \(\textrm{expit}\big(\hat{\beta}_{0} + \hat{\beta}_{age}\times \textrm{age} + \hat{\beta}_{smk}\times \textrm{smoke} \pm 1.64\hat{\sigma}_{u0} \big)\), where \(\textrm{expit}(x) = 1/(1 + e^{-x})\)

  • One way to interpret the variation visually is to randomly generate many values of \(p_{ij}( u_{i} )\) using the estimated distribution of \(u_{i}\) to simulate the values of \(u_{i}\).

    • This can help us to get a sense of how much variability there is in wheezing probability across individuals.

  • To do this, I simulated values of \(p_{ij}( u_{i} )\) for each combination of age/smoking status and plotted the results in 8 densities in 4 panels.

    • It would probably be better to use some sort of bounded density estimator for these plots.
beta.hat <- coef(summary(ohio.intercept))[,1]
n <- 1000
pneg2.smoke <- plogis(rnorm(n,sd=2.34) + beta.hat[1] - 2*beta.hat[2] + beta.hat[3]) #age -2 with smoke
pneg2 <- plogis(rnorm(n, sd=2.34) + beta.hat[1] - 2*beta.hat[2]) #age -2 w/o smoke
pneg1.smoke <- plogis(rnorm(n,sd=2.34) + beta.hat[1] - 1*beta.hat[2] + beta.hat[3]) #age -1 with smoke
pneg1 <- plogis(rnorm(n, sd=2.34) + beta.hat[1] - 1*beta.hat[2]) # age -1 w/o smoke
p0.smoke <- plogis(rnorm(n, sd=2.34) + beta.hat[1] + beta.hat[3]) # age 0 with smoke
p0 <- plogis(rnorm(n, sd=2.34) + beta.hat[1]) # age 0 w/o smoke
p1.smoke <- plogis(rnorm(n,sd=2.34) + beta.hat[1] + beta.hat[2] + beta.hat[3]) # age 1 with smoke
p1 <- plogis(rnorm(n, sd=2.34) + beta.hat[1] + beta.hat[2]) # age 1 w/o smoke

par(mfrow=c(2,2), mar=c(4.1, 4.1, .5, .5))
plot(density(pneg2), lwd=2, xlab = "Probability of Wheezing at Age 7", main="", col="red")
d <- density(pneg2.smoke)
lines(d$x, d$y, lwd=2)
legend("topright", legend = c("Smoke", "No Smoke"), col=c("black", "red"), bty='n', lwd=2)
plot(density(pneg1), lwd=2, xlab = "Probability of Wheezing at Age 8", main="", col="red")
d <- density(pneg1.smoke)
lines(d$x, d$y, lwd=2)
legend("topright", legend = c("Smoke", "No Smoke"), col=c("black", "red"), bty='n', lwd=2)
plot(density(p0), lwd=2, xlab = "Probability of Wheezing at Age 9", main="", col="red")
d <- density(p0.smoke)
lines(d$x, d$y, lwd=2)
legend("topright", legend = c("Smoke", "No Smoke"), col=c("black", "red"), bty='n', lwd=2)
plot(density(p1), lwd=2, xlab = "Probability of Wheezing at Age 10", main="", col="red")
d <- density(p1.smoke)
lines(d$x, d$y, lwd=2)
legend("topright", legend = c("Smoke", "No Smoke"), col=c("black", "red"), bty='n', lwd=2)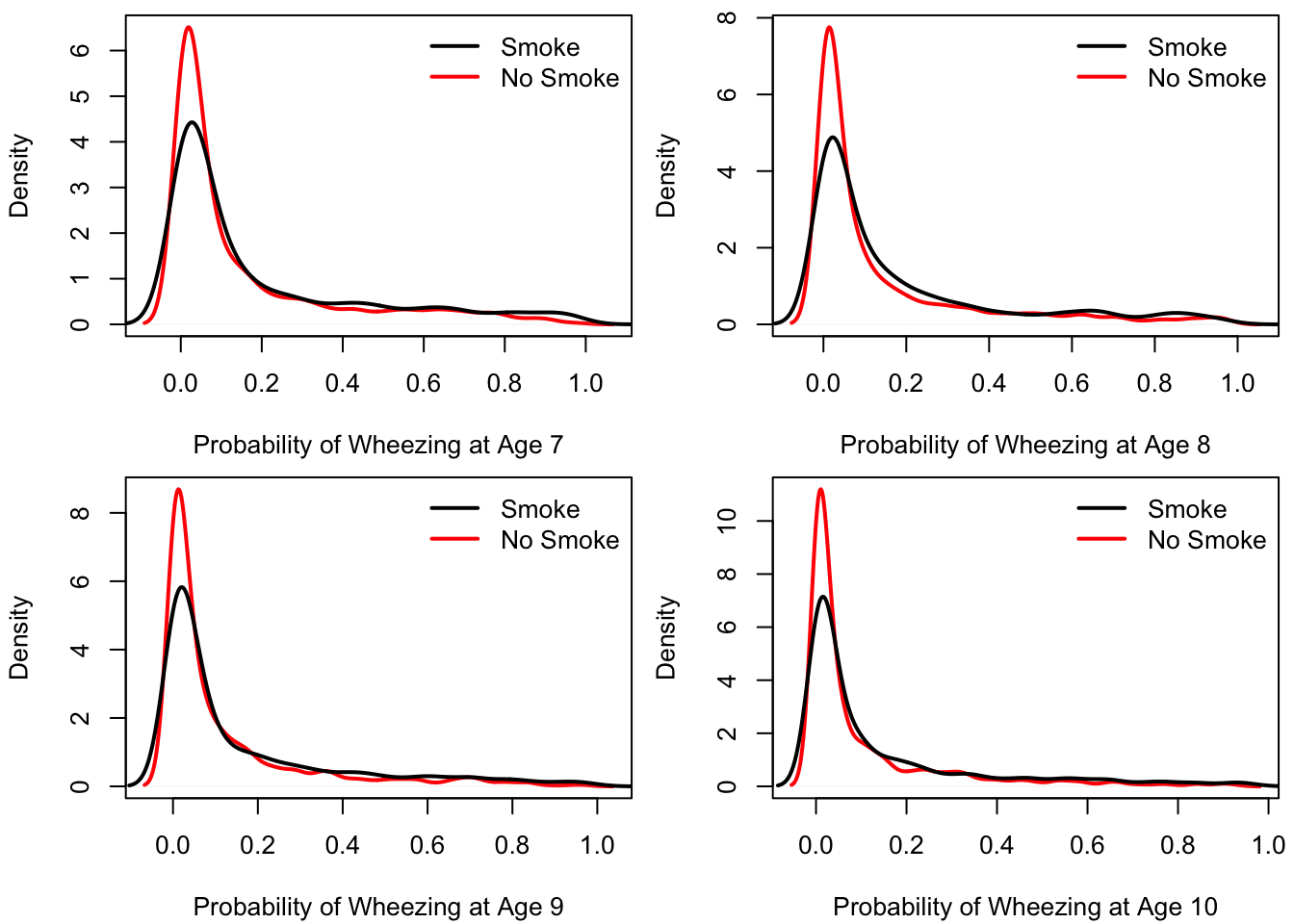
Distribution of Wheezing probability across individuals for different values of age and smoking status

Figure 1.4: Distribution of Wheezing probability across individuals for different values of age and smoking status

1.6 Exercises

  • For these exercises, you will use the actg_trial dataset. This dataset was obtained from https://content.sph.harvard.edu/fitzmaur/ala2e/cd4-data.txt.
    • I also placed this dataset in a file named actg_trial.csv inside the Data folder on Canvas.
  • When you load the dataset into R, it should look like the following
head( actg_trial, 10)
##    SubjectID Treatment     Age Sex    Week      CD4
## 1          1         2 36.4271   1  0.0000 3.135494
## 2          1         2 36.4271   1  7.5714 3.044522
## 3          1         2 36.4271   1 15.5714 2.772589
## 4          1         2 36.4271   1 23.5714 2.833213
## 5          1         2 36.4271   1 32.5714 3.218876
## 6          1         2 36.4271   1 40.0000 3.044522
## 7          2         4 47.8467   1  0.0000 3.068053
## 8          2         4 47.8467   1  8.0000 3.891820
## 9          2         4 47.8467   1 16.0000 3.970292
## 10         2         4 47.8467   1 23.0000 3.610918
  • This longitudinal dataset has 5036 observations with the following 6 variables:
    • SubjectID - subject identifier
    • Treatment - treatment received (4 possible treatments)
    • Age - age in years at baseline
    • Sex - 1=M, 0=F
    • Week - time in weeks from baseline
    • CD4 - this is the natural logarithm of the CD4 count + 1

1.6.1 Questions

  • How many individuals are in the trial?

  • What are the smallest and largest values of \(n_{i}\) in this data set?

  • Ignoring the longitudinal correlation, try fitting the linear model \[\begin{equation} Y_{ij} = \beta_{1} + \gamma_{1}t_{ij} + \sum_{j=2}^{4}\beta_{j}I(Trtment = j) + \sum_{j=2}^{4}\gamma_{j}t_{ij}I(Trtment = j) + e_{ij} \tag{1.5} \end{equation}\] where \(Y_{ij}\) is the value of CD4 of subject \(i\) at time \(t_{ij}\) and where \(t_{i1}, ..., t_{in_{i}}\) are the values of the Week variable for person \(i\).

  • For model (1.5), what is the interpretation of \(\beta_{1}\), \(\beta_{2}\), \(\beta_{3}\), \(\beta_{4}\)?

  • What are the interpretations of \(\beta_{2} - \beta_{1}\), \(\beta_{3} - \beta_{1}\), and \(\beta_{4} - \beta_{1}\)? If this is a randomized trial, what do you expect the values of \(\beta_{2} - \beta_{1}\), \(\beta_{3} - \beta_{1}\), \(\beta_{4} - \beta_{1}\) will be?

  • In model (1.5), what is the interpretation of \(\gamma_{1}\)?

  • In model (1.5), what term represents the change in CD4 from time 0 to 24 weeks for those assigned to treatment 2? What is the standard error for this term?

  • Now account for longitudinal correlation by fitting a mixed model to the actg_trial dataset. Try fitting the following mixed model \[\begin{equation} Y_{ij} = u_{i} + \beta_{1} + \gamma_{1}t_{ij} + \sum_{j=2}^{4}\beta_{j}I(Trtment = j) + \sum_{j=2}^{4}\gamma_{j}t_{ij}I(Trtment = j) + e_{ij}, \end{equation}\] where \(u_{i}\) is a subject-specific random intercept term?

  • For this model, what is the dimension of the “Z matrix” returned by lmer?

  • How do the estimates \(\beta_{1}\), \(\beta_{2}\), \(\beta_{3}\), \(\beta_{4}\) compare with the model which did not have any random effects?

  • Now, try fitting a mixed effects model with random intercepts and slopes using lmer: \[\begin{equation} Y_{ij} = u_{i0} + u_{i1}t_{ij} + \beta_{1} + \gamma_{1}t_{ij} + \sum_{j=2}^{4}\beta_{j}I(Trtment = j) + \sum_{j=2}^{4}\gamma_{j}t_{ij}I(Trtment = j) + e_{ij} \end{equation}\]

  • Use the anova function to perform a likelihood ratio test of the random intercept vs. the random intercept + slope model.

References

Diggle, Peter, Patrick Heagerty, Kung-Yee Liang, and Scott Zeger. 2013. Analysis of Longitudinal Data. Vol. 25.